LS-PLM
非线性化分割
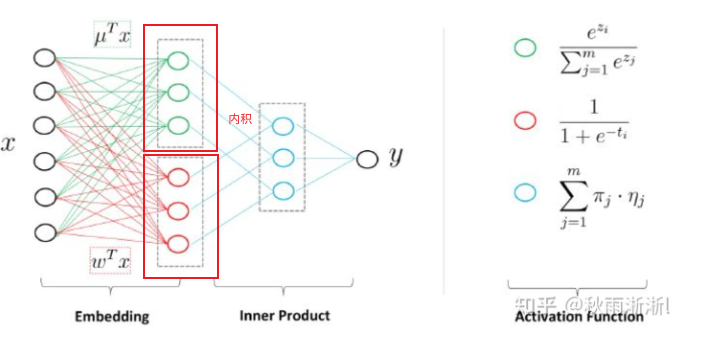
LS-PLM模型也称为MLR(混合逻辑回归),它的结构类似于三层神经网络(三层神经网络包含的隐藏层具有非线性变换的能力,通常通过激活函数实现),他的输入层是样本的特征向量,中间层是由m个神经元组成的隐层(m是模型的分片数量,通过控制m来控制分片数,防止过拟合)
传统的LR线性模型只能对样本进行线性分割,而LS-PLM在深度学习到来之前,已经将线性模型提升为非线性模型,实现了模型端到端的非线性学习能力。
其中的非线性化主要是通过softmax函数(也就是\(\pi_i(x)\))将特征切分到m个不同的空间,并由LR部分(也就是\(\eta_i(x)\))对m个空间的特征进行线性学习来实现的。
其中随着m的增长,需要的样本数也增加,阿里推荐的值为\(m=12\)。
最终的预估函数\(f(x)\)为:
\[f(x) = \sum_{i=1}^{m} \pi_i(x) \cdot \eta_i(x)=\sum_{i=1}^{m} \frac{e^{\eta_i(x)}}{\sum_{j=1}^{m} e^{\eta_j(x)}}\cdot \frac{1}{1+e^{-w_i\cdot x}}\]

所以实际上,LS-PLM模型也可以看做是一个三层的神经网络模型:
- 第一层:输入层,也指样本的特征向量
- 第二层:隐层,通过两个激活函数相乘实现非线性化,实现了Embedding操作
- 其中第一个激活函数实现聚类,包含m个神经元
- 聚类的原因:不同的人群具有聚类特性,同一类人群具有类似的广告点击偏好
- 第二个激活函数实现LR分类,包含m个神经元
- 隐藏层输出为m维切片
- 其中第一个激活函数实现聚类,包含m个神经元
- 第三层:输出层,包含单一神经元
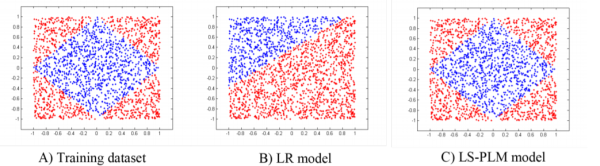
如下图所示,LR不能拟合非线性数据,MLR可以拟合非线性数据(m=4,实现4切片)
解决稀疏性问题:代价函数加入正则化
LS-PLM主要是通过\(L_1\)和\(L_{2,1}\)正则化来做到这件事情。其中 \(L_{2,1}\)用于实现特征筛选,\(L_1\)则用于得到尽可能多的稀疏解。
目标损失函数为:

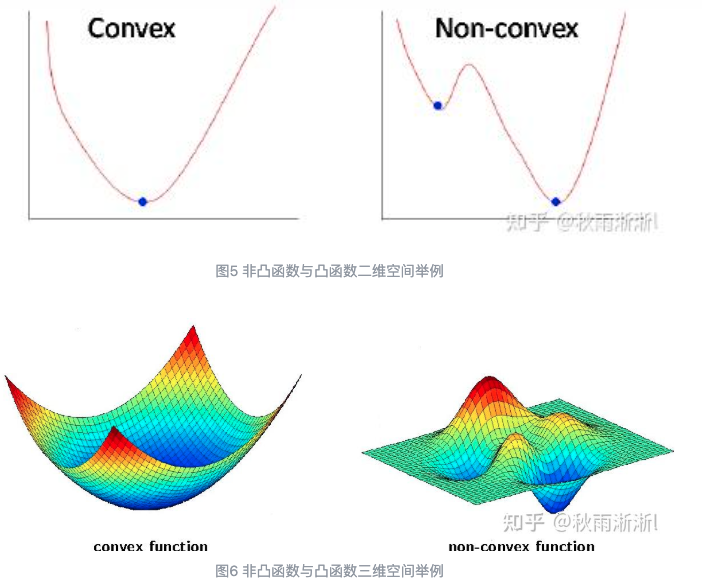
此时由于\(L_1\)和\(L_2\)正则化函数都是非平滑的,所以损失函数是非凸函数(不止一个极值点),所以可能求得的结果是局部最优解而非全局最优解。
参考: