本文假设有n个特征
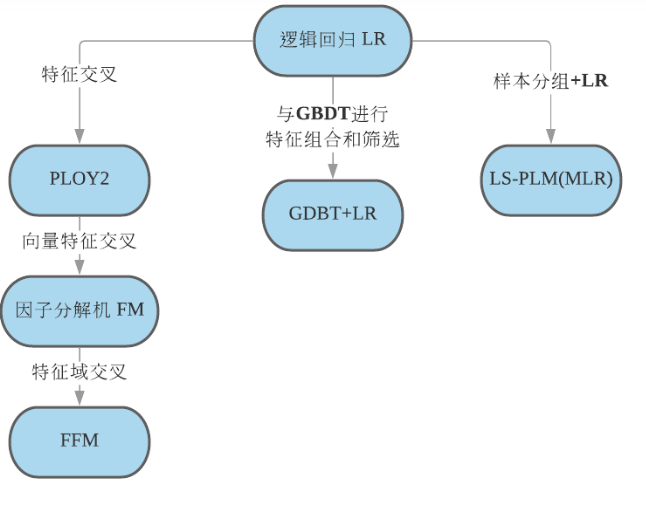
一、POLY2模型
前面学到的逻辑回归模型只对多维特征进行简单线性加权,没有多维特征的组合(逻辑回归模型只能通过工程师手动组合特征)。
而POLY2模型、FM模型、FFM模型具备特征交叉的能力,其表达能力更强。
传统的逻辑回归模型的预测函数为:
\[y=w_0+\sum_{i}^n w_i x_i\]
POLY2模型会为每个特征组合赋予一个权重,因此其n个特征需要\(n^2\)个参数。其复杂度为\(O(n^2)\),预测结果在线性模型的基础上多了一个多项式:
\[y=\sum_{i=1}^{n-1}\sum_{j=i+1}^n w_{i,j} x_i x_j\]
缺点:
这种属于暴力组合,由于互联网数据本身通过one-hot成的稀疏数据,因此通过暴力组合增加维度后会更加稀疏,导致模型计算量剧增、泛化能力差。
解决办法:可以通过矩阵分解出隐向量的方式来降低计算量、提高模型泛化能力。FM模型就是通过这种方式构建的。
二、FM模型
关于特征分解隐向量的相关基础知识参考博客推广搜2:传统推荐模型之协同过滤算法
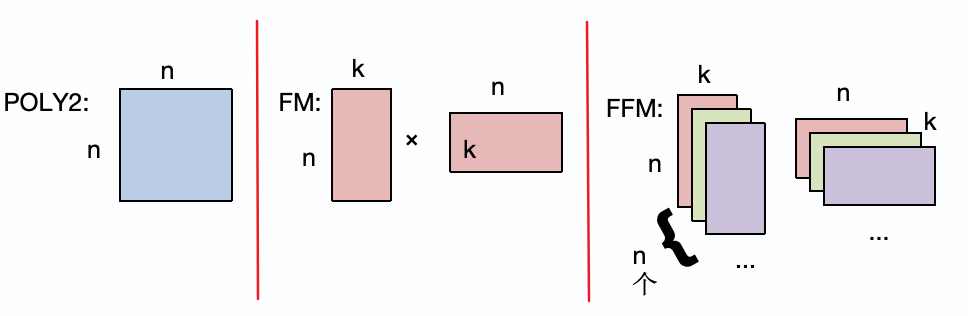
POLY2为每个特征组合赋予一个权重,相当于每个特征都有一个对应其他所有特征的向量组合,也就是向量矩阵大小为\(n\times n\)。
FM模型则通过矩阵分解的方式将特征向量分解为隐向量,其隐向量大小为\(n\times k\),每两个特征向量的权值\(w_ij\)是由这两个向量的隐向量内积计算而得的:
\[w_{ij}=\mathbf{v_i}\mathbf{v_j^T}\]
因此带入到前面的POLY2模型中,FM的预测函数为:
\[y=\sum_{i=1}^{n-1}\sum_{j=i+1}^n \mathbf{v_i}\mathbf{v_j^T} x_jx_j\]
三、FFM模型
FM模型中,每个特征向量\(v_i\)都只有一个隐向量,也就是说,当某个特征\(i\)跟其他任意特征\(j\)交互时,发挥的都是相同的作用(因为使用的是同一个隐向量\(\vec{v_i}\)。
但是很多时候一个特征对不同特征发挥的作用效果是不同的,为了解决这个问题,FFM提出了域field的概念,也就是将每个特征从一个隐向量扩展为每个特征有一组隐向量,缺点是这也增加了计算复杂度,从FM模型到FFM模型复杂度由\(O(nk)\)变为\(O(n^2k)\)。
FFM模型的预测函数为:
\[y=\sum_{i=1}^{n-1}\sum_{j=i+1}^n\mathbf{v_{i,f_j}}\mathbf{v_{j,f_i}^T} x_jx_j\]
其中\(\mathbf{v_{i,f_j}}\)表示在总共存在的n个隐向量矩阵中,特征\(i\)作用于特征\(j\)上对应的隐向量为第\(j\)张矩阵的第\(i\)行。
缺点:FM和FFM一般只能做到二阶特征交叉(也就是特征两两交叉),由FM的二阶变为三阶,其模型参数计算量剧增。
解决办法:通过如GBDT+LR的组合模型来解决高阶特征交叉的问题。
参考