一、基础知识
1.1 梯度下降
梯度下降也称为最速下降法,其目的是找到一个函数的局部极小值。
梯度下降法:
假设需要根据已有的样本拟合一函数\(f_\theta(t_1, t_2, ..., t_n)= \theta_1t_1 + \theta_2t_2 + ... + \theta_nt_n\),其中\(t_1, t_2, ..., t_n\)为样本的特征值,\(\theta_1, \theta_2, ..., \theta_n\)为各个特征对应的权重。
那么我们需要做的就是根据已有样本集迭代找出各个\(\theta_i\)的取值,使得能拟合出函数\(f\):
找到令代价函数(损失函数)\(J(\theta_1, \theta_2, ..., \theta_n)\) 的最小点。其中代价函数通常是表示预测值与真实值之间的误差。
由于\(J(\theta_1, \theta_2, ..., \theta_n)\)是多维的,因此针对每个维度\(\theta_i\),其偏导数\(\frac{\partial J}{\partial \theta_i}\),也称为梯度,在该维度下,变量\(\theta_i\)沿梯度的反方向移动时,损失函数下降最快。基于此,令步长为\(\alpha\),则各个\(\theta_i\)的更新公式为:
\[ \theta_i = \theta_i - \alpha \frac{\partial J}{\partial \theta_i} \]
举例说明梯度下降法的运作:
假设有一个函数\(y = f_w(x) = w_1x + w_2\),针对该函数,有一些样本集:\(x_1, x_2, ..., x_m\),其对应的标签值:\(y_1, y_2, ..., y_m\)。
需要通过梯度下降法不断更新\(w_1, w_2\)并找到最优的\(w_1, w_2\),从而拟合函数\(f_w(x)\):
首先找到\(f\)函数的损失函数:
\[J(w_1, w_2) = \frac{1}{2m}\sum_{i=1}^m(f_w(x_i) - y_i)^2\]
对\(w_1\)的更新方向是对\(w_1\)维度求它在\(j(w_1,w_2)\)函数中的偏导(对\(w_2\)的更新同理):
\[\frac{\partial J}{\partial w_1} = \frac{1}{m}\sum_{i=1}^m(f_w(x_i) - y_i)x_i\]
令更新步长为\(\alpha\),则\(w_1\)的更新公式为:
\[w_1 = w_1 - \alpha \frac{\partial J}{\partial w_1} \]
在梯度下降法的一个epoch中,会先初始化\(w_1, w_2\),然后不断重复上述步骤更新\(w_1, w_2\),直到\(J(w_1, w_2)\)的值满足要求(最小化\(J(w_1, w_2)\))。
1.2 极大似然估计
假设上述提到要拟合的函数\(f\)为概率密度函数,那么他的代价函数需要用极大似然估计来刻画拟合的匹配程度。
似然函数:
1)离散型模型:
\[L(\theta) = \prod_{i=1}^m p_\theta(X_i=x_i)\]
2)连续型模型:
\[L(\theta) = \prod_{i=1}^m f_\theta(x_i)\]
举例说明极大似然估计:
假设我们有一个要拟合的高斯概率密度函数:
\[f_{\mu,\sigma^2}=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
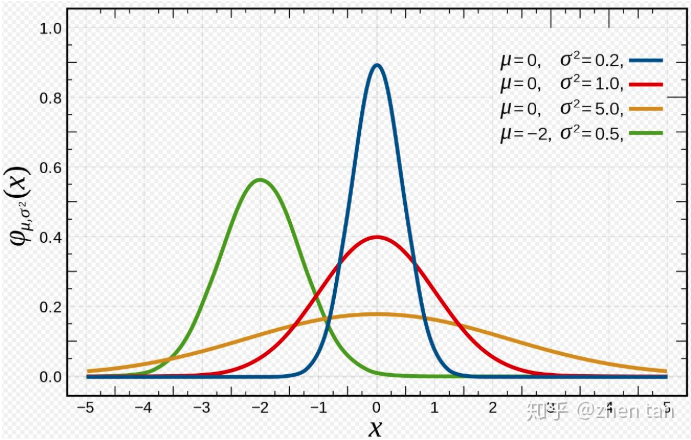
针对该函数,我们有样本集:\(x_1, x_2, ..., x_m\),将所有样本集带入待拟合函数中并相乘可以获得对应的似然函数(也就是代价函数):
\[L(\mu,\sigma^2)=\prod_{i=1}^m f_{\mu,\sigma^2}(x_i)\]
其中由于似然函数就是概率的乘积,而样本点取出大概率时间的概率比较高,似然函数越大时说明这些点在某个模型中概率越大,那就说明这个模型就是最接近真实分布的,那对应的参数自然就是目标参数
因此越接近真实函数的\(\mu,\sigma^2\),其似然函数\(L(\mu,\sigma^2)\)的值越大。所以我们的参数求解目标就是\((\mu^*, \sigma^*)=argmaxL(\mu,\sigma^2)\)。
由于是求最大值,因此可以给似然函数加上一个递增函数\(\ln\),使其由相乘变成相加:
\[L(\mu,\sigma^2)=\ln\prod_{i=1}^m f_{\mu,\sigma^2}(x_i)=\sum_{i=1}^m \ln f_{\mu,\sigma^2}(x_i)\]
似然函数的最大值点处的梯度是0,因此可以求出最大值点:
\[ \frac{\partial L}{\partial \mu} = 0\]
\[ \frac{\partial L}{\partial \sigma^2} = 0\]
以此来求得\((\mu^*, \sigma^*)\)的更新公式。
参考:
二、逻辑回归算法
2.1 区分两类推广搜模型
在推广搜的算法中,通常模型会分为以协同过滤为代表的相似性推荐模型和以逻辑回归为代表的分类模型:
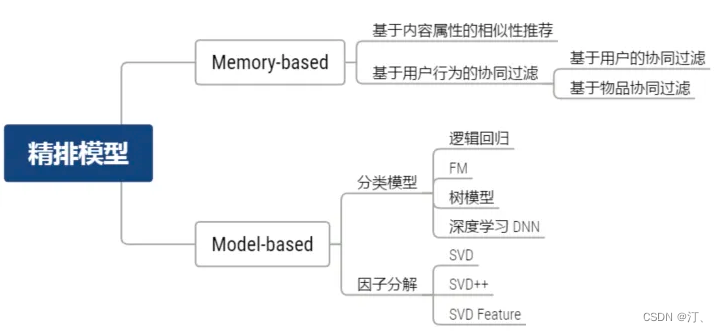
协同过滤模型:
是利用用户和物品的相互行为信息进行推荐的,只需要相互行为信息而不是特征信息;它是一种基于相似度的推荐算法。
逻辑回归模型:
是综合考虑了用户、物品、场景的特征信息,依赖特征提取、实现多特征融合;它是基于概率分类的推荐算法。
2.2 逻辑回归算法原理
1)确定待拟合函数\(f\)
由于实际情况中,我们并不能准确地先给定一个待拟合的函数\(f\),因此,在逻辑回归中我们将推荐问题转换成了CTR点击率预估问题,也就是预测一个样本的点击率,将样本映射到\([0,1]\)之间
因此给定输入神经元是根据权重累和各个特征值,其中的权重和常数b就是待拟合的参数,同时通过激活函数sigmoid将输出映射到\([0,1]\)之间:
\[f_\mathbf{w}(\mathbf{x_i}) = \frac{1}{1 + e^{-\mathbf{w·x_i}+b}}\]
整个拟合函数如下所示:
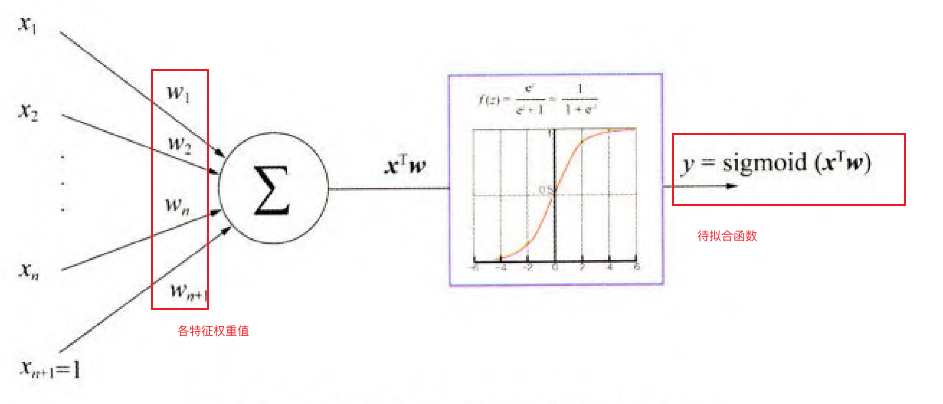
经过拟合后,最终输出结果为正样本(类别为1:推荐)和负样本(类别为0:不推荐),因此我们需要给输入的样本也添加一个类别标签\(y_i\),其值为0或1,0表示不推荐,1表示推荐。则该拟合函数的概率模型为:
\[p(y_i=1|\mathbf{x_i}) = f_\mathbf{w}(\mathbf{x_i})\] \[p(y_i=0|\mathbf{x_i}) = 1 - f_\mathbf{w}(\mathbf{x_i})\]
上述拟合函数的概率模型也可以合并起来表示:
\[p(y_i|\mathbf{x_i}) = (f_w(\mathbf{x_i}))^y(1-f_w(\mathbf{x_i}))^{1-y}\]
2)确定损失函数\(J\)
由极大似然估计可知,拟合函数的拟合匹配程度是由似然函数刻画的,其似然函数为:
\[L(\mathbf{w}) = \prod_{i=1}^m p(y_i|\mathbf{x_i})\]
由于代价函数一般是求最小值问题,而似然函数是求最大值问题,因此需要将似然函数转化为最小化问题,也就是乘上系数\(-\frac{1}{k}\),并取对数\(ln\)转换成连加,最终得到代价函数为:
\[J(\mathbf{w}) = -\frac{1}{k}\sum_{i=1}^m p(y_i|\mathbf{x_i})\]
3)确定参数更新公式
对代价函数\(J(\mathbf{w})\)求偏导,并按步长\(\alpha\)更新参数:
\[w_j = w_j - \alpha \frac{\partial J(\mathbf{w})}{\partial w_j}\]
其中:
\[\frac{\partial J(\mathbf{w})}{\partial w_j} = \frac{1}{k}\sum_{i=1}^m(f_w(\mathbf{x^i}) - y^i)x^i_j\]