一、基础知识
1.1 正则化
正则化是通过给损失函数添加正则项来减少噪点的影响,防止过拟合的
作用:避免某些离奇数据影响训练,防止训练过拟合。也就是避免拟合离奇数据。
1.2 过拟合
过拟合是指训练拟合结果虽然能拟合所有样本数据,但是由于离奇样本数据的存在,导致拟合结果与实际不符合
过拟合的可能原因:
- 训练次数epoch过多
- 训练数据集过少
- 特征过多,未筛选
- 没有引入正则化约束,导致模型的鲁棒性和泛化能力差...
过拟合的缺点:导致训练结果不稳定
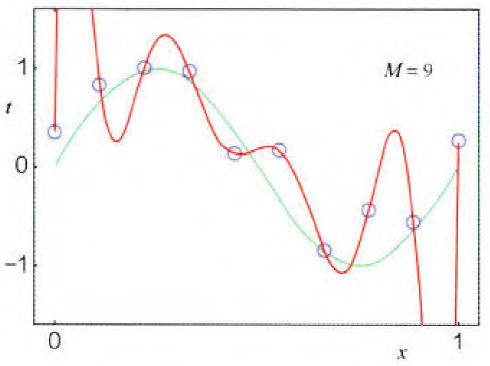
过拟合的例子如下图所示,红色线为过拟合结果,把噪声点也拟合进去了;蓝色线是加入正则化后得到的正常拟合结果,噪声点没被拟合进去:
二、协同过滤算法
协同过滤算法可以分为userCF和itemCF两种,假设有m个用户,n种物品:
userCF:基于用户相似,算法会为用户推荐与用户兴趣相似的用户喜欢的物品
通过生成**m*m大小的用户相似性矩阵来进行推荐,考虑与用户兴趣相似的用户的意见。但是由于现实互联网中,用户数量远大于物品数量,因此会导致相似性矩阵的计算量过大,现实使用中通常选择itemCF方法**。
itemCF:基于物品相似,算法会为用户推荐与用户历史喜欢物品相似的物品
通过生成**n*n大小的物品相似性矩阵**来进行推荐,通过用户历史喜欢的物品,结合物品相似性矩阵来推荐。
协同过滤的缺点:
- 当用户数量远大于物品数量时,用户相似性矩阵的计算量过大
- 在低频场景下,用户历史数据稀疏,找到相似用户困难
可以考虑使用矩阵分解来优化计算量并缓解矩阵稀疏问题。
2.1 userCF算法实现
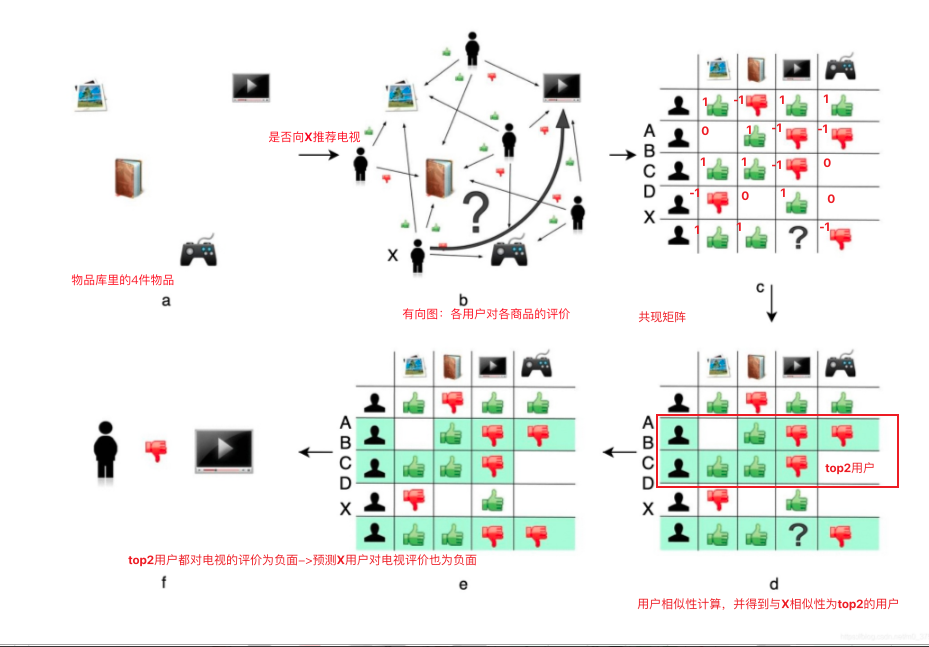
userCF协同过滤算法主要分为5个过程:
1)物品库中有n个物品,用户有m个;
2)用户历史评价有向图;
3)协同过滤的共现矩阵;
通过将点赞值映射为1,踩值为-1,未点赞值为0,得到物品库中物品之间的共现矩阵
4)计算用户相似性矩阵并排出topk作为推荐目标;
计算用户i和用户j的相似度,其实就是计算用户向量i和用户向量j之间的相似度(也就是第i行跟第j行)。通常可以选择采用余弦相似度计算两向量的夹角来表示用户相似度。
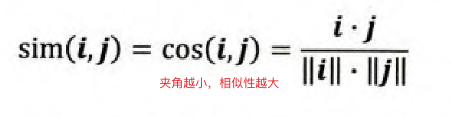
- 皮尔逊相关系数:添加用户平均分进行修正,减少用户评分偏置的影响

- 基于皮尔逊相关系数引入物品平均分,减少物品评分偏置的影响
- 皮尔逊相关系数:添加用户平均分进行修正,减少用户评分偏置的影响
5)利用相关系数topk的用户对目标物品的评价来最终预测是否推荐给用户

userCF协同过滤流程图:
2.2 itemCF算法实现
相比userCF,itemCF在构建相似性矩阵和预测结果函数上有所不同。
- 相似性矩阵:通过物品i列向量和物品j列向量之间的相似度来计算物品相似度矩阵,得到n*n大小的物品相似矩阵。
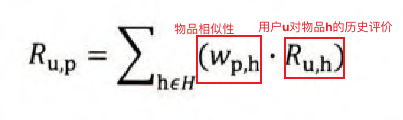
- 预测结果函数:通过物品相似矩阵和用户历史物品评分的累和来预测用户对目标物品的评分。
三、矩阵分解
3.1 算法原理
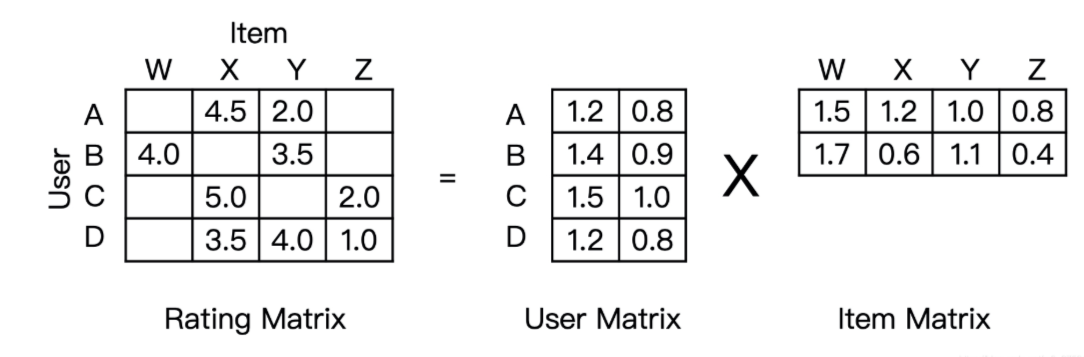
矩阵分解为每个用户和物品生成隐向量并映射到多维坐标中,在坐标中离用户近的物品就是推荐目标。
也就是将mn的共现矩阵分解为mk的用户矩阵和**k*n的物品矩阵**,其中k为隐向量维度。
最后某个用户对某个物品的评价(也就是共现矩阵的值)可以通过用户矩阵和物品矩阵计算预测出来。
矩阵分解的优点:
- 泛化能力强,一定程度上解决矩阵稀疏问题
- 空间复杂度低,从n^2降低到(n+m)*k
- 矩阵分解结果便于与其他特征拼接组合
- 便于与深度学习网络无缝结合
矩阵分解的缺点:
- 与协同过滤矩阵一样,不方便加入用户、物品、场景等特征
可以通过逻辑回归模型通过因子分解融合多种特征。
3.2 梯度下降
如何分解共现矩阵呢?
通常采用的是梯度下降方法来获取物品向量矩阵q和用户向量矩阵p。
其中损失函数的制定是要让共现矩阵的值r与分解结果(p*q)的差值最小,对损失函数求导找到梯度方向,根据偏导更新权重。同时加上正则化,因此最终的损失函数为:
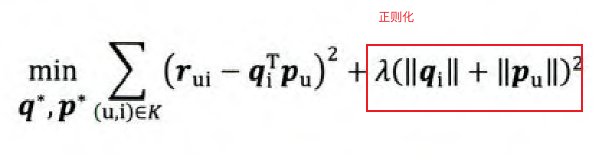
参考
书籍: 《深度学习推荐系统》