AkiraZheng's Time.

排序实现

Word count: 3.2kReading time: 13 min
2024/04/03

一、选择排序

选择排序是一种简单直观的排序算法。它的工作原理如下：

  • 遍历数组以[i,end]作为未排序序列，找到最小值的下标minIndex。
  • 不断重复：在当前轮次未排序序列中找到最小（大）元素，存放到当前轮次排序序列的起始位置。

1.1 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void selectSort(vector<int>& vec) {
	//选择排序
	if (vec.size() == 0 || vec.size() == 1) return;

	int vec_size = vec.size();
	for (int i = 0; i < vec_size-1; ++i) {
		int k = i;//记录当前轮次最小值的索引
		for (int j = i; j < vec_size; ++j) {
			if (vec[j] < vec[k]) {
				//找到新的最小点了
				k = j;
			}
		}
		//一轮下来找到最小值后进行交换
		swap(vec[i], vec[k]);
	}
}

1.2 测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template <typename T>
void printVec(vector<T>& v) {
	for (auto x : v) {
		cout << x << " ";
	}
}

int main() {
	vector<int> vec{ 23,1,23,5,1,4,13,7,1 };
	selectSort(vec);
	printVec(vec);

	return 0;
}

1.3 复杂度分析

时间复杂度：O(n^2)

空间复杂度：O(1)，属于原地排序。

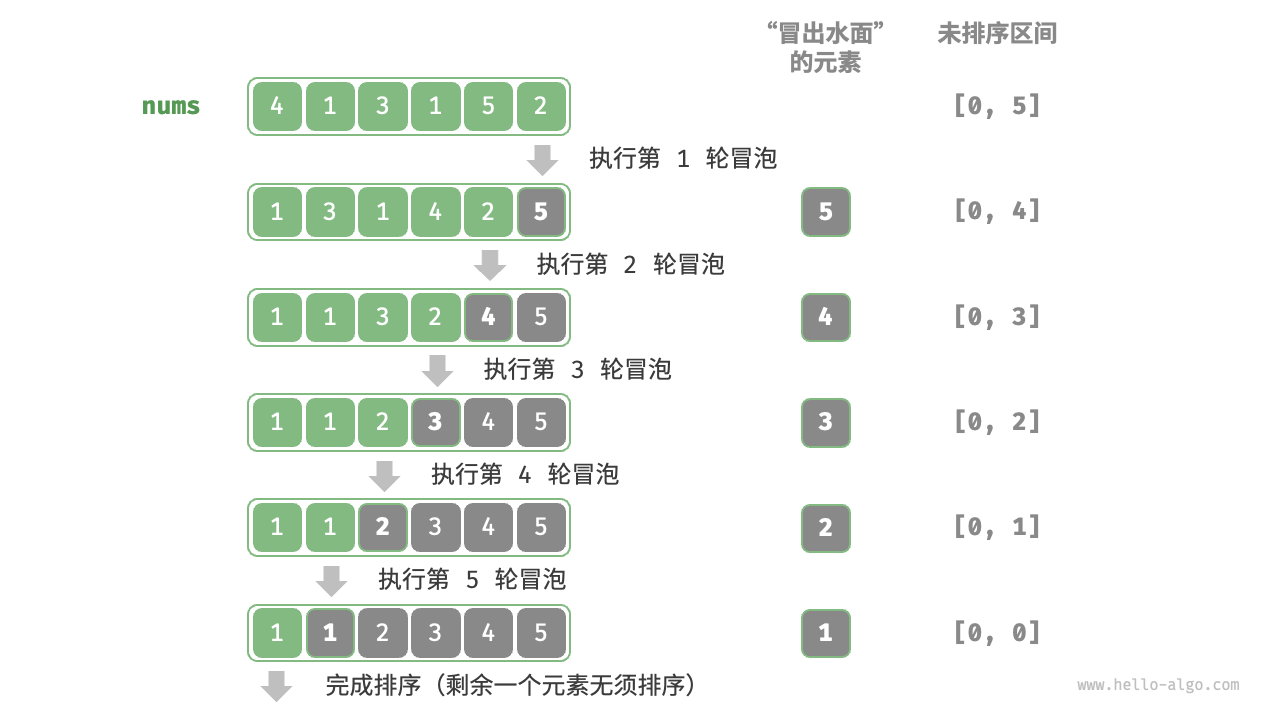
二、冒泡

选择排序是记录最小值的下标，一轮下来后将最小值排在最前面；

而冒泡排序是一轮中不断地进行判断与两两交换，最后将最大值排在最后面。它的实现原理为：

  • 从头开始，两两比较相邻元素，如果逆序则交换。
  • 重复上述步骤，直到没有任何一对数字需要比较。

2.1 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void bubbleSort(vector<int>& vec) {
	//冒泡排序

	int vec_size = vec.size();
	if (vec_size == 0 || vec_size == 1) return;

	for (int i = vec_size - 1; i > 0; --i) {
		//从index为最末尾开始（也就是找到最大值）
		for (int j = 0; j < i; ++j) {
			if (vec[j] > vec[j + 1]) {
				swap(vec[j], vec[j + 1]);
			}
		}
	}
}

2.2 测试

1
2
3
4
5
6
7
int main() {
	vector<int> vec{ 23,1,23,5,1,4,13,7,1 };
	bubbleSort(vec);
	printVec(vec);

	return 0;
}

2.3 优化

  • 如果某一轮下来没有发生交换，说明已经有序，可以提前结束排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void bubbleSort(vector<int>& vec) {
	//冒泡排序

	int vec_size = vec.size();
	if (vec_size == 0 || vec_size == 1) return;

	for (int i = vec_size - 1; i > 0; --i) {
		//从index为最末尾开始（也就是找到最大值）	
		bool swapFlag = false; //记录当前轮有没有发生了交换
		for (int j = 0; j < i; ++j) {
			if (vec[j] > vec[j + 1]) {
				swap(vec[j], vec[j + 1]);
				swapFlag = true;
			}
		}
		//优化：一轮下来没有发生交换，
		if (!swapFlag) {
			//没发生交换，已经有序了
			cout << "轮次：" << vec_size - i << endl;
			return;
		}
	}
}

2.4 复杂度分析

时间复杂度和空间复杂度跟选择排序一样。

时间复杂度：O(n^2)，在优化下，若数组已经有序，时间复杂度为O(n)。

空间复杂度：O(1)，属于原地排序。

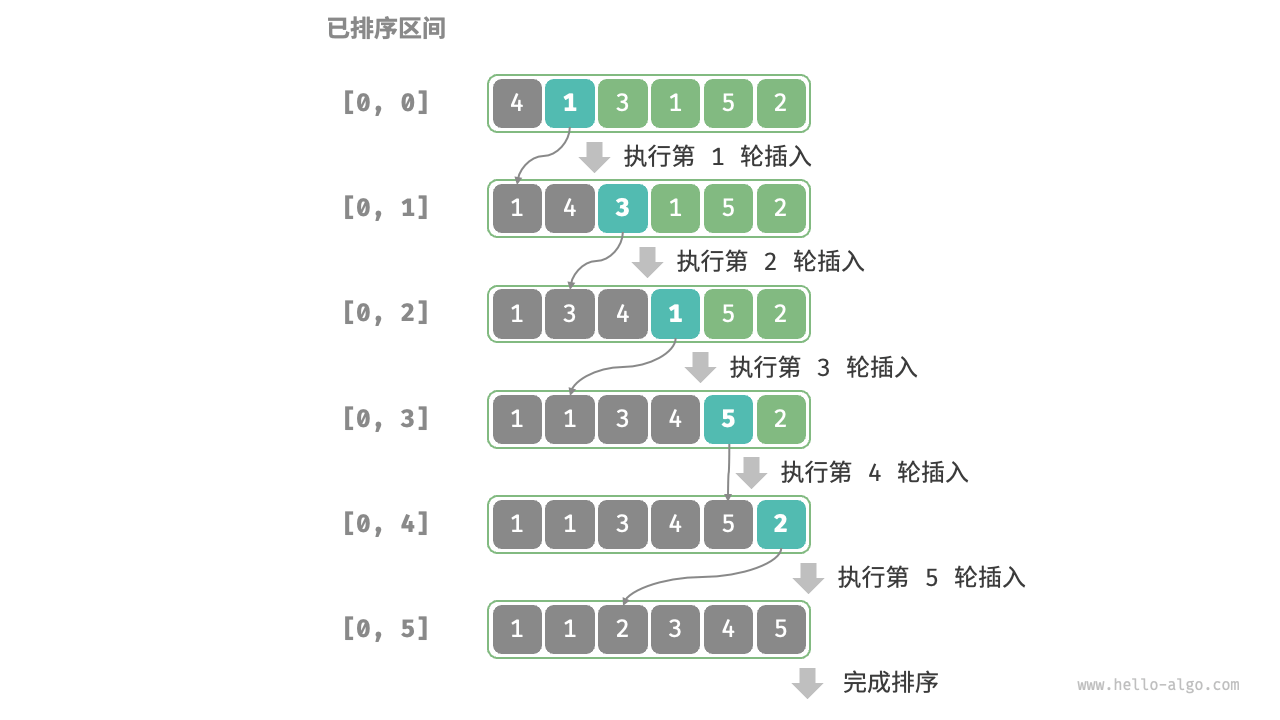
三、插入排序

插入排序是一种简单直观的排序算法，其思想与扑克牌排序类似。它的工作原理如下：

  • 从第一个元素开始，该元素可以认为已经被排序。
  • 取出下一个元素j，在已经排序的元素序列中从后向前扫描，扫描范围为k=[j-1,0]。
  • 如果vec[j] < vec[k]，则将vec[k]向后移动一个位置，直到找到前面已排序数组中第一个vec[j] >= vec[k]。

3.1 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void insertSort(vector<int>& vec) {
	//插入排序

	int vec_size = vec.size();
	if (vec_size == 0 || vec_size == 1) return;

	for (int i = 1; i < vec_size; i++) {//默认第一个数已排序
		//保证前i个数是已排序的
		//循环直到找到前i个数中第一个比其小的数
		int val = vec[i];
		int j = i - 1;
		while (j >= 0 && vec[j] >= val) {
			//vec[j]较大，需要后移一位
			vec[j + 1] = vec[j];
			j--;
		}
		vec[j + 1] = val;
	}
}

3.2 复杂度分析

时间复杂度：O(n^2)，在数组本身已经有序的情况下，时间复杂度为O(n)。

空间复杂度：O(1)，属于原地排序。

四、快速排序

快速排序是一种分治的排序算法。它通过将一个数组分成两个子数组，将左右两部分独立地不断递归实现排序。

本文参考的是B站上的一个Up主的思路，但是代码是原创实现的。全网最清晰快速排序，看完快排思想和代码全部通透，不通透你打我！

4.1 思路

  • 选择一个基准值，将数组分成两部分，左边的值都小于基准值，右边的值都大于基准值。
  • 递归地对左右两部分进行排序。

4.2 代码实现

4.2.1 根据视频实现

  • 先实现一个分区函数quickSort_midpos，将数组分成两部分，左边的值都小于基准值，右边的值都大于基准值。并返回基准值的位置用于下一轮左右两部分的递归排序。
  • 递归函数quickSort不断调用quickSort_midpos对左右两部分进行排序。
  • 设计静态函数myQuickSortTest用于测试。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#pragma once
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
class myQuickSort
{
public:
	void printVect(vector<int>& arr) {
		for (int num : arr) {
			cout << num << " ";
		}
		cout << endl;
	}

    //快速排序:递归实现
	void quickSort(vector<int> &arr, int left, int right) {
		if (right > left) {
			//递归方法实现对arr的原地排序
			//printVect(arr);
			int pos = quickSort_midpos(arr, left, right);//放回当前层归类左右两边后的中心点位置

			//继续对中心点位置的左右两边进行快排
			quickSort(arr, left, pos - 1);//左边递归排序
			quickSort(arr, pos + 1, right);//右边递归排序
		}
	}

    //快速排序:分区函数
	int quickSort_midpos(vector<int>& arr, int left, int right) {
		int pos_val = arr[left];//取左边第一个点作为分界线（空点，等待比起小的点填补进去

		int empty_index = left;//其实不是empty，该位上的值为pos_val
		while (left != right) {
			if (empty_index == left) {
				//空值在左边，需要移动右边的点，找到比分界线小的点进行交换
				if (arr[right] <= pos_val) {
					//右边的值是比分界线小的值，需要移到empty位置
					swap(arr[empty_index], arr[right]);
					//更新新的空值为right
					empty_index = right;
					left++;
				}
				else {
					//右边的值比分界线大，继续移动右边的指针直到找到比分界线小的值
					right--;
				}
			}
			else if (empty_index == right) {
				//此时空值在右边，需要移动左指针，找到比分界线大的点进行交换
				if (arr[left] >= pos_val) {
					swap(arr[left], arr[empty_index]);
					empty_index = left;
					right--;
				}
				else {
					left++;
				}
			}
		}

		//将分界值传回数组中
		arr[left] = pos_val;
		return right;//也可传回right
	}

    //测试函数
	static void myQuickSortTest() {

		cout << "Please input some nums(int) and use exit to stop inputting numbers:" << endl;

		vector<int> arr;

		int num;
		string strIn;
		while (cin >> strIn) {
			if (strIn == "exit") {
				break;
			}
			try
			{
				num = stoi(strIn);

				//检查转成int后的数再转成string是否还跟原始输入的值一样，是的话则说明输入值是个整数，否则抛出一个错误
				if (to_string(num) != strIn) {
					cout << "Error!! Please input a num(int) again!" << endl;
				}
				else {
					arr.push_back(num);
				}
			}
			catch (const std::exception&)
			{
				cout << "Invalid Input! Please input a num(int) again!" << endl;
			}
		}

		//vector<int> arr = { 13,435,1,54,7,23,7,2,76,12,0 };

		myQuickSort QS;
		QS.quickSort(arr, 0, arr.size() - 1);
		QS.printVect(arr);

		cout << "调试用" << endl;

	}
};

测试

1
2
3
4
5
#include "myQuickSort.h"
int main() {
    myQuickSort::myQuickSortTest();
    return 0;
}

4.2.2 根据Hello算法实现

Hello算法中的思想更为简单明了，在一个[left,right]范围内查找pos时的思路为：

  • 以第一个数nums[left]作为基准值base，将双指针分别赋值为low = left和high = right
  • 从右向左移动high，找到第一个小于base的数
  • 从左向右移动low，找到第一个大于base的数
  • 交换nums[low]和nums[high]
  • 重复上述步骤，直到low和high相遇，相遇后就剩最后一个位置需要交换，将base和nums[low]交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//
// Created by MacBook pro on 24-9-21.
//

#ifndef QUICKSORT_H
#define QUICKSORT_H

#include <iostream>
#include <vector>

using namespace std;


class quicksort {
public:
    //将区间[left, right]内的数据根据基准值nums[left]进行划分，左边全部小于等于基准值，右边全部大于等于基准值
    int position(vector<int>&nums, int left, int right) {
        //当前排序的范围是[left, right]

        //选择基准值
        int baseNum = nums[left];
        int low = left;
        int high = right;
        while(low < high) {
            //以刚开始的left作为基准时：必须得先从右边找起，不然会出现最后baseNum跟比baseNum大的值交换，导致左边出现比baseNum大的值
            //从右边找到第一个比baseNum小的数
            //从左边找到第一个比baseNum大的数
            //将找到的两个数进行交换
            while(low < high && nums[high] >= baseNum) --high;
            while(low < high && nums[low] <= baseNum) ++low;
            swap(nums[low], nums[high]);
        }

        //将基准值放至分区位置
        swap(nums[left], nums[low]);

        return low;
    }

    //进行地柜排序
    void doQuickSort(vector<int> &nums, int left, int right) {
        //当前排序的范围是[left, right]
        if(left >= right) return;

        //获取当前分区的基准值的位置
        int pos = position(nums, left, right);
        //继续排左边的
        doQuickSort(nums, left, pos - 1);
        //继续排右边的
        doQuickSort(nums, pos+1, right);
    }
};

#endif //QUICKSORT_H

代码中的position函数是用来找到基准值的位置，quickSort函数是递归调用position函数对左右两部分进行排序。

4.3 复杂度分析

时间复杂度：O(nlogn)，最坏情况下为O(n^2)。

空间复杂度：最坏情况是O(n)，在输入数组完全倒序的情况下，达到最差递归深度n，使用O(n)栈帧空间。

4.4 快排为什么快？

  • 出现最坏情况的概率很低
  • 快速排序快的主要原因是大大减少了比较和交换的次数，因为按基准数切分的两半数组，在一个数组里面的数据是绝对不会和第二个数组里面的数字产生比较的机会的，所以大幅度降低了做无用功的机会。

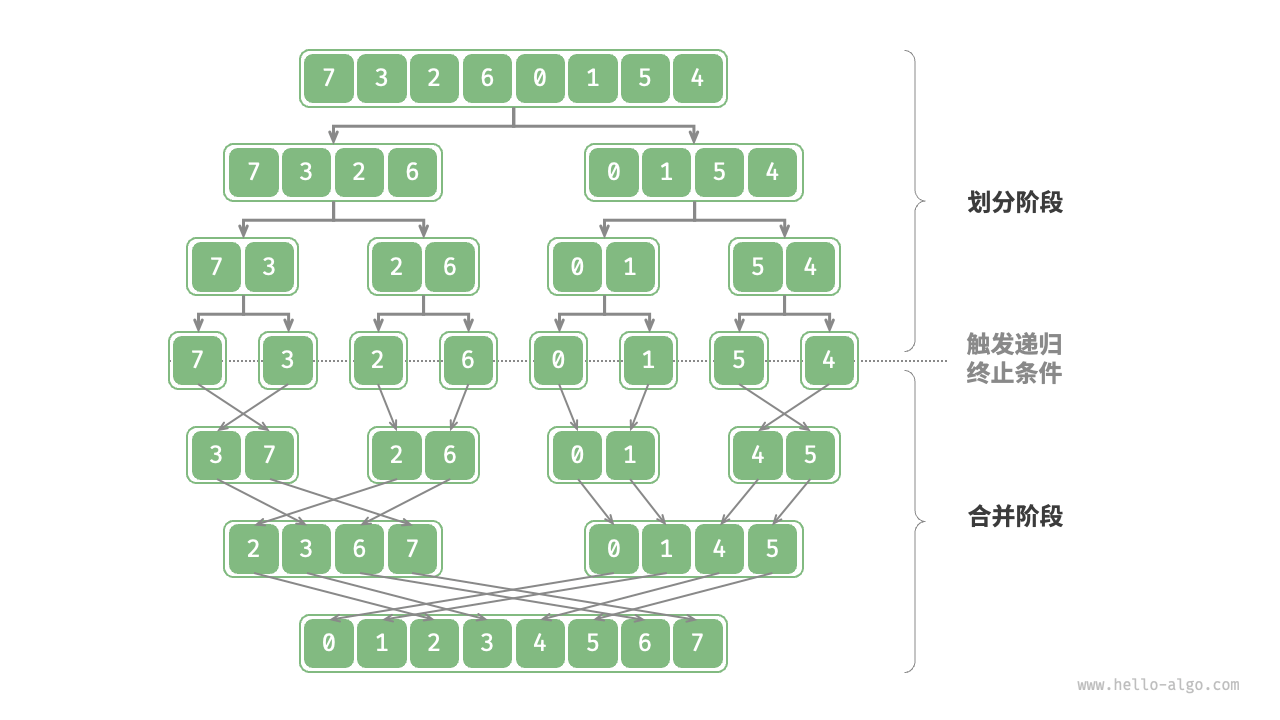
五、归并排序

5.1 思路

归并排序是一种分治的排序算法，思想是先按照左右中的顺序，具体步骤如下：

  • 左右：先不断递归地将数组分成两半，直到每个子数组只有一个元素后return回溯，得到某一层的左右两个有序数组（默认一个元素是有序的）
  • 中：将左右两个有序数组合并成一个有序数组，期间需要用到临时数组来存放合并后的有序数组

5.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
void merge(vector<int>& vec, int left, int right) {

	int LR_size = right - left + 1;
	vector<int> tmpVec(LR_size);

	//通过临时数组&&比对数值合并左右子树
	int mid = (left + right) / 2;//[left,mid]是左边，[mid+1,right]是右边
	int left_p = left, right_p = mid+1;
	int i = 0;
	while(left_p <= mid && right_p <= right) {//以左树为基准进行数据填充，且两个子树都还没遍历到最后的点
		if (vec[left_p] <= vec[right_p]) {
			//左子树值更小，将左子树值放入
			while (left_p<=mid && vec[left_p] <= vec[right_p]) {
				tmpVec[i++] = vec[left_p++];
				/*++i;
				++left_p;*/
			}
		}
		else {
			//右子树值更小，将右子树值放入
			while (right_p <= right && vec[left_p] > vec[right_p]) {
				tmpVec[i++] = vec[right_p++];
			}
		}
	}

	//将剩下的左/右子树添加到数组中
	if (left_p <= mid) {
		//右子树走完了，剩下的都填充给左子树
		while (left_p <= mid) {
			tmpVec[i++] = vec[left_p++];
		}
	}
	else if (right_p <= right) {
		//左子树走完了，剩下的都填充给右子树
		while (right_p <= right) {
			tmpVec[i++] = vec[right_p++];
		}
	}

	//将临时数组赋值给原始数组
	left_p = left;
	for (auto tmp : tmpVec) {
		vec[left_p++] = tmp;
	}
}

void mergeSort(vector<int>& vec, int left, int right) {
	if (left >= right) return;

	//递归分左右子树
	int mid = (left + right) / 2;
	mergeSort(vec, left, mid);
	mergeSort(vec, mid+1, right);

	//merge合并左右子树
	//左/右 子树是已经排序了的
	merge(vec, left, right);
}

5.3 复杂度分析

时间复杂度：O(nlogn)，划分产生高度为lg(n)的递归树，每层合并的总操作数量为O(n)

空间复杂度：O(n)，合并操作需要一个临时数组来存放合并后的有序数组。

六、堆排序

6.1 思路

未完待续......

七、总结

各种算法的复杂度总结：

参考：Hello 算法

Author：AkiraZheng

Link：https://akirazheng.github.io/2024/04/03/%E6%8E%92%E5%BA%8F%E5%AE%9E%E7%8E%B0/

Publish date：April 3rd 2024, 9:28:27 pm

Update date：October 4th 2024, 1:59:59 am

License：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 一、选择排序
    1. 1.1 代码实现
    2. 1.2 测试
    3. 1.3 复杂度分析
  2. 二、冒泡
    1. 2.1 代码实现
    2. 2.2 测试
    3. 2.3 优化
    4. 2.4 复杂度分析
  3. 三、插入排序
    1. 3.1 代码实现
    2. 3.2 复杂度分析
  4. 四、快速排序
    1. 4.1 思路
    2. 4.2 代码实现
      1. 4.2.1 根据视频实现
      2. 4.2.2 根据Hello算法实现
    3. 4.3 复杂度分析
    4. 4.4 快排为什么快？
  5. 五、归并排序
    1. 5.1 思路
    2. 5.2 代码实现
    3. 5.3 复杂度分析
  6. 六、堆排序
    1. 6.1 思路
  7. 七、总结
Total : 59
2025
2024
2023
2022
计算机 杂货铺-休闲 环境配置 深度学习 任务调度项目
C++知识点 重装-环境配置-计算机 计算机网络 数据结构与算法 数据库 WebServer项目（C++） 系统设计 深度学习算法 操作系统 设计模式 任务调度项目